Đề thi chất lượng cao lớp 7 môn toán THCS Bích Hòa năm 2014
06/08/2014 15:14 pm
Đề thi chất lượng cao môn toán lớp 7 trường THCS Bích Hòa năm 2014 có đáp án được cập nhật chiều ngày 6/8/2014. Các em tham khảo dưới đây.
Đề thi chất lượng cao môn toán lớp 7 trường THCS Bích Hòa năm 2014
Câu 1:( 5điểm): Cho a) b) c)
Câu 2: (2 điểm): Tìm x; y biết:
Câu 3:(4 điểm) a).Chứng minh rằng : . b) Tìm số nguyên a để:
Câu 4: (2 điểm): Tìm giá trị lớn nhất của biểu thức sau:
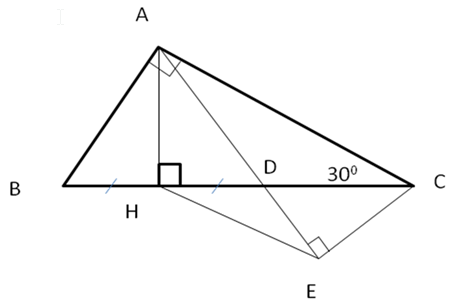
Câu 5: (7 điểm) Cho tam giác ABC vuông ở A, có góc C = 300, đường cao AH. Trên đoạn HC lấy điểm D sao cho HD = HB. Từ C kẻ CE vuông góc với AD. Chứng minh: a) Tam giác ABD là tam giác đều. b) AH = CE. c) EH song song với AC. Đáp án đề thi chất lượng cao môn toán lớp 7 trường THCS Bích Hòa năm 2014Câu 1:( 5điểm) a) Từ (0,5điểm)
b) Từ khi đó
c) Theo câu b) ta có: từ hay vậy
Câu 2: (2điểm) Tìm các số x;y biết.
Áp dụng tính chất của dãy tỉ số bằng nhau ta có: => => -x = 5x -12 => x = 2. (0,5điểm) Thay x = 2 vào trên ta được
=> 1+ 3y = -12y => 1 = -15y => y = -1/15 (0,5điểm) Vậy x = 2, y = -1/15 thỏa mãn đề bài. Câu 3:(4 điểm) a). Đặt Ta có : * *
Vậy:
b. Ta có :
là số nguyên (1 điểm) Khi đó (a + 3) là ước của 14 mà Ư(14) = ±1; ±2; ±7; ±14 Ta có : a = -2;- 4;- 1; - 5; 4 ; - 10; 11 ; -17 (1 điểm)
Câu 4: Tìm giá trị lớn nhất của biểu thức sau:
A < 0 với mọi giá trị của x nên A đạt giá trị lớn nhất khi |A|đạt giá trị nhỏ nhất
|x| ≥ 0 với mọi x nên |x| + 1996 ≥ 1996 (1 điểm) Vậy |A| nhỏ nhất bằng 1996/1997 khi x = 0 (0,5 điểm) Suy ra GTLN của A = -1996/1997 khi x = 0 (0,5 điểm)
Câu 5: (7 điểm)
Nguồn dethi.violet.vn NẮM CHẮC KIẾN THỨC, BỨT PHÁ ĐIỂM 9,10 LỚP 1 - LỚP 12 CÙNG TUYENSINH247! Nếu em đang:
Tuyensinh247 giúp em:
Xem thêm thông tin khoá học & Nhận tư vấn miễn phí - TẠI ĐÂY |
||||
Viết bình luận: Đề thi chất lượng cao lớp 7 môn toán THCS Bích Hòa năm 2014
- Đề thi thử TN THPT lần 1 năm 2026 môn Hóa - Cụm chuyên môn số 10 Hải Phòng (03/02/2026)
- Nội dung ôn tập giữa kì 2 Văn lớp 10 - THPT Trần Phú-Hoàn Kiếm 2026 (21/01/2026)
- Nội dung ôn tập giữa kì 2 lớp 10 môn Anh 2026 - THPT Trần Phú-Hoàn Kiếm (21/01/2026)
- Đề thi học kì 1 lớp 7 môn KHTN 2025 - THCS Phú An (15/01/2026)
Tin tức mới nhất
- Môn thi thứ 3 vào lớp 10 Hà Tĩnh năm 2026
- Danh sách tỉnh công bố môn thi thứ 3 vào lớp 10 năm 2026
- Danh sách trường công bố đề án tuyển sinh 2026 - Mới nhất
- Thông tin tuyển sinh trường Đại học Công nghệ Đông Á 2026
- Thông tin tuyển sinh trường Đại học Bình Dương 2026
- Thông tin tuyển sinh trường Đại học Tiền Giang 2026