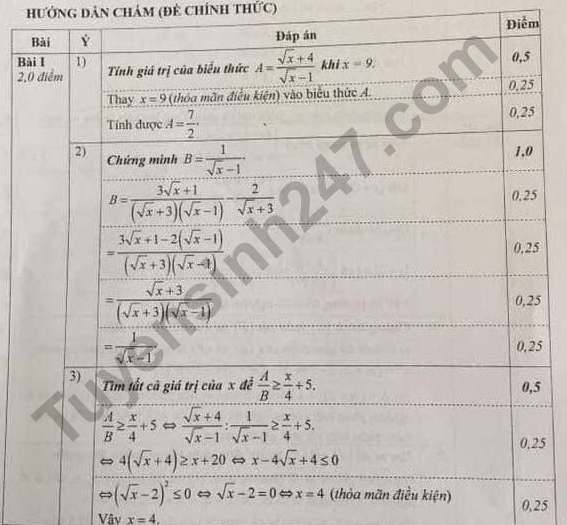
Đáp án đề thi vào lớp 10 môn Toán Hà Nội 2018

Đề thi vào lớp 10 môn Toán Hà Nội năm 2018

Bài IV. (3,5 điểm)

Cho đường tròn (O;R) với dây cung AB không đi qua tâm. Lấy S là một điểm bất kì trên tia đối của tia AB (S khác A). Từ điểm S vẽ hai tiếp tuyến SC, SD với đường tròn (O;R) sao cho điểm C nằm trên cung nhỏ AB (C, D là các tiếp điểm). Gọi H là trung điểm của đoạn thẳng AB.

1)      Chứng minh năm điểm C, D, H, O, S thuộc đường tròn đường kính SO.

2)      Khi SO = 2R, hãy tính độ dài đoạn thẳng SD theo R và tính số đo góc CSD .

3)      Đường thẳng đi qua điểm A và song song với đường thẳng SC, cắt đoạn thẳng CD tại điểm K. Chứng minh tứ giác ADHK là tứ giác nội tiếp và đường thẳng BK đi qua trung điểm của đoạn thẳng SC.

4)      Gọi E là trung điểm của đoạn thẳng BD và F là hình chiếu vuông góc của điểm E trên đường thẳng AD. Chứng minh rằng, khi điểm S thay đổi trên tia đối của tia AB thì điểm F luôn thuộc một đường tròn cố định.

Xem thêm: Đáp án môn Văn thi sáng nay tại đây 

Hướng dẫn giải đề thi vào lớp 10 môn Toán Hà Nội 2018

Xem đáp án đề thi vào lớp 10 môn Toán của Sở GD Hà Nội đầy đủ tại đây

Theo TTHN