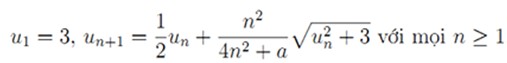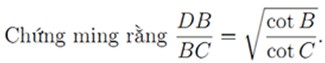Đề thi học sinh giỏi quốc gia THPT môn Toán năm 2015

Kỳ thi chọn học sinh giỏi quốc gia THPT năm 2015

Môn: Toán

Thời gian: 180 phút (không kể thời gian giao đề)

Ngày thi: 8/1/2015

Câu 1. Cho a là một số thực không âm và (u_n) là dãy số xác định bởi:

a) Với a = 0, chứng minh dãy số có giới hạn hữu hạn và tìm giới hạn đó.

b) Với mọi a ∈ [0,1], chứng minh dãy số có giới hạn hữu hạn.

Câu 2. Cho a, b, c là các số thực không âm. Chứng minh rằng

3(a² + b² + c²) ≥ (a + b + c) (√ab + √bc + √ca) + (a – b)² + (b – c)² + (c – a)² ≥ (a + b + c)²

Câu 3. Cho số nguyên dương K. Tìm số tự nhiên n không vượt qua 10K thỏa mãn đồng thời các điều kiện sau:

1) n chia hết cho 3

2) Các chữ số trong biểu diễn thập phân của n thuộc tập hợp {2, 0, 1, 5}

Câu 4. Cho đường tròn (O) và hai điểm B, C cố định trên (O), BC không là đường kính. Một điểm A thay đổi trên (O) sao cho tam giác ABC nhọn. Gọi E, F lần lượt là chân đường cao kẻ từ B, C của tam giác ABC. Cho (I) là đường tròn thay đổi đi qua E, F và có tâm là I.

a) Giả sử (I) tiếp xúc với BC tại điểm D.

b) Giả sử (I) cắt cạnh BC tại hai điểm M, N. gọi H là trực tâm tam giác ABC và P, Q là các giao điểm của (I) với đường tròn ngoại tiếp tam giác HBC. Đường tròn (K) đi qua P,Q và tiếp xúc với (O) tại điểm T (T cùng phía A đối với PQ). Chứng minh rằng đường phân giác trong của góc MTN đi qua một điểm cố định.

Đáp án được Tuyensinh247 cập nhật sau.

Để ôn luyện tốt môn Toán trong kỳ thi THPT Quốc gia năm 2015, các em tham khảo tại đây: http://tuyensinh247.com/hoc-truc-tuyen-mon-toan-c47.html

Tuyensinh247 tổng hợp