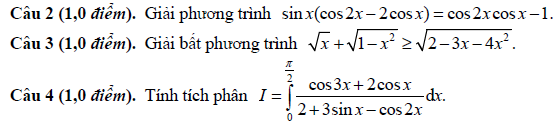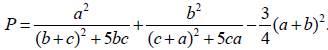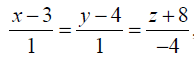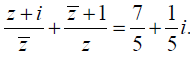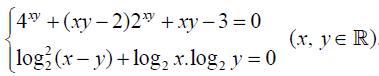Đề thi thử đại học môn Toán khối A,A1 năm 2014 lần cuối THPT chuyên ĐH Vinh
24/06/2014 11:42 am
Tuyensinh247 cập nhật đề thi thử đại học môn Toán khối A,A1 lần cuối năm 2014 THPT chuyên ĐH Vinh các em theo dõi dưới đây.
ĐỀ THI THỬ ĐẠI HỌC MÔN TOÁN KHỐI A,A1 LẦN CUỐI NĂM 2014 CHUYÊN ĐH VINHI. PHẦN CHUNG CHO TẤT CẢ THÍ SINH (7,0 điểm) Câu 1 (2,0 điểm). Cho hàm số y = -x - 1/(x - 1) a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số đã cho. b) Viết phương trình tiếp tuyến của đồ thị (C) tại điểm M, biết khoảng cách từ điểm M đến đường thẳng ∆ : y = 2 x -1 bằng 3/√5.
Câu 5 (1,0 điểm). Cho hình hộp ABCD.A 'B 'C' D ' có đáy ABCD là hình thoi cạnh a√3, BD = 3a, hình chiếu vuông góc của B lên mặt phẳng (A 'B 'C ' D ') là trung điểm của A'C '. Biết rằng côsin của góc tạo bởi hai mặt phẳng ( ABCD) và (CDD'C') bằng √21/7. Tính theo a thể tích khối chóp ABCDA'B'C'D' và bán kính mặt cầu ngoại tiếp tứ diện A' BC ' D '. Câu 6 (1,0 điểm). Giả sử a, b, c là các số thực dương thỏa mãn a + b + c = 1. Tìm giá trị nhỏ nhất của biểu thức
II. PHẦN RIÊNG (3,0 điểm) Thí sinh chỉ được làm một trong hai phần (phần a hoặc phần b) a. Theo chương trình Chuẩn Câu 7.a (1,0 điểm). Trong mặt phẳng với hệ tọa độ Oxy, cho hình bình hành ABCD có phương trình đường chéo AC : x - y + 1 = 0, điểm G(1; 4) là trọng tâm của tam giác ABC, điểm E(0; - 3) thuộc đường cao kẻ từ D của tam giác ACD. Tìm tọa độ các đỉnh của hình bình hành đã cho biết rằng diện tích của tứ giác AGCD bằng 32 và đỉnh A có tung độ dương. Câu 8.a (1,0 điểm). Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC vuông tại C, góc BAC = 30o, AB = 3√2 , đường thẳng AB có phương trình
, đường thẳng AC nằm trên mặt phẳng (α): x + z - 1 = 0. Tìm tọa độ các đỉnh của tam giác ABC biết rằng đỉnh B có hoành độ dương. Câu 9.a (1,0 điểm). Tìm số phức z thỏa mãn
b. Theo chương trình Nâng cao Câu 7.b (1,0 điểm). Trong mặt phẳng với hệ tọa độ Oxy, cho hình thang ABCD có AD // BC, AD = 2BC đỉnh B(4; 0), phương trình đường chéo AC là 2x - y - 3 = 0, trung điểm E của AD thuộc đường thẳng ∆ : x - 2 y + 10 = 0. Tìm tọa độ các đỉnh còn lại của hình thang đã cho biết rằng cot góc ADC = 2. Câu 8.b (1,0 điểm). Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(2; 1; 1), B(3; 2; 4) và mặt phẳng (α) : x + 5 y -2z -5 = 0. Tìm điểm M thuộc mặt phẳng (a) sao cho MA ⊥ AB và d (A , MB) = √(330/31), Câu 9.b (1,0 điểm). Giải hệ phương trình
ĐÁP ÁN ĐỀ THI THỬ ĐẠI HỌC MÔN TOÁN KHỐI A,A1 LẦN CUỐI NĂM 2014 CHUYÊN ĐH VINH
Các em chú ý theo dõi các đề thi thử đại học môn Toán khối A,A1 tiếp theo trên Tuyensinh247 nhé! Tuyensinh247 tổng hợp NẮM CHẮC KIẾN THỨC, BỨT PHÁ ĐIỂM 9,10 LỚP 1 - LỚP 12 CÙNG TUYENSINH247! Nếu em đang:
Tuyensinh247 giúp em:
Xem thêm thông tin khoá học & Nhận tư vấn miễn phí - TẠI ĐÂY |
>> Đề thi thử đại học môn Toán khối A,A1,B năm 2014 tỉnh Hải Dương
>> Đề thi thử đại học môn Toán khối A,A1 năm 2014 lần 5 THPT chuyên Bắc Ninh
Viết bình luận: Đề thi thử đại học môn Toán khối A,A1 năm 2014 lần cuối THPT chuyên ĐH Vinh
- Đề thi thử TN THPT 2026 môn Địa - THPT Lê Viết Thuật (05/03/2026)
- Đề thi thử vào lớp 10 năm 2026 môn Toán - THCS Hưng Dũng lần 1 (05/03/2026)
- Đề thi thử TN THPT lần 2 năm 2026 môn Địa - Cụm 13 trường THPT Hải Phòng (05/03/2026)
- Đề thi thử TN THPT năm 2026 môn Văn - Liên trường THPT Nghệ An (05/03/2026)
Tin tức mới nhất
- Thông tin tuyển sinh trường Sĩ quan chính trị năm 2026
- Danh sách trường công bố đề án tuyển sinh 2026 - Mới nhất
- Thông tin tuyển sinh Đại học Mỹ thuật Công nghiệp Hà Nội 2026
- Nghiên cứu khả năng mở phân hiệu đại học Hàn Quốc tại Việt Nam
- Danh sách trường Đại học xét học bạ THPT 2026 - Mới nhất
- Thông tin tuyển sinh trường Đại học Hoa Sen 2026