Đề thi thử đánh giá năng lực ĐHQG Hà Nội có đáp án - Tuyensinh247 số 2

CẤU TRÚC BÀI THI

-----------------------------------------

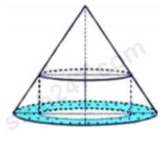
NỘI DUNG BÀI THI

BIÊN SOẠN: BAN CHUYÊN MÔN TUYENSINH247.COM

PHẦN I - TƯ DUY ĐỊNH LƯỢNG

Câu 1: Trong không gian với hệ tọa độ \(Oxyz,\) cho hai đường thẳng \({d_1}:{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \dfrac{x}{2} = \dfrac{{y - 1}}{1} = \dfrac{{z + 1}}{{ - 2}}\) và \({d_2}:{\mkern 1mu} {\mkern 1mu} \dfrac{{x - 1}}{1} = \dfrac{{y - 2}}{2} = \dfrac{{z - 3}}{{ - 2}}.\) Khoảng cách giữa hai đường thẳng này bằng

A. \(\dfrac{{\sqrt {17} }}{{16}}\) 

B. \(\dfrac{{\sqrt {17} }}{4}\) 

C. \(\dfrac{{16}}{{\sqrt {17} }}\) 

D. 16

Câu 2: Diện tích hình phẳng giới hạn bởi đường thẳng \(y = x + 3\) và parabol \(y = 2{x^2} - x - 1\) bằng

A. 9 

B. \(\dfrac{{13}}{6}\) 

C. \(\dfrac{{13}}{3}\) 

D. \(\dfrac{9}{2}\)

Câu 3: Đề thi trắc nghiệm môn Toán gồm 50 câu hỏi, mỗi câu có 4 phương án trả lời trong đó chỉ có một phương án trả lời đúng. Mỗi câu trả lời đúng được 0,2 điểm. Một học sinh không học bài nên mỗi câu trả lời đều chọn ngẫu nhiên một phương án. Xác suất để học sinh đó được đúng 5 điểm là:

A.  \(\dfrac{{C_{50}^{25}{{\left( {\dfrac{1}{4}} \right)}^{25}}.{{\left( {\dfrac{3}{4}} \right)}^{25}}}}{{{4^{50}}}}\). 

B.  \(C_{50}^{25}{\left( {\dfrac{1}{4}} \right)^{25}}.{\left( {\dfrac{3}{4}} \right)^{25}}\). 

C.  \({\left( {\dfrac{1}{4}} \right)^{25}}.{\left( {\dfrac{3}{4}} \right)^{25}}\). 

D.  \(\dfrac{{\dfrac{{25}}{4}.{{\left( {\dfrac{3}{4}} \right)}^{25}}}}{{{4^{50}}}}\).

Câu 4: Cho hàm số \(y = {x^3} - m{x^2} - {m^2}x + 8.\) Có bao nhiêu giá trị nguyên của m để hàm số có điểm cực tiểu nằm hoàn toàn phía bên trên trục hoành? 

A. 3  

B. 5  

C. 4  

D. 6 

Câu 5: Có bao nhiêu giá trị nguyên của m để hàm số \(y = \dfrac{{mx + 4}}{{x + m}}\) nghịch biến trên khoảng \(\left( { - 1;{\mkern 1mu} {\mkern 1mu} 1} \right)?\)

A. 4 

B. 2 

C. 5 

D. 0 

Câu 6: Trong không gian Oxyz, cho hai điểm \(A( - 1;0;0)\),\(B(2;0;1)\). Tọa độ của vecto \(\overrightarrow {AB} \) là

A. \(\overrightarrow {AB} {\rm{ \;}} = (3;0;1)\)  

B. \(\overrightarrow {AB} {\rm{ \;}} = ( - 2;0; - 1)\) 

C. \(\overrightarrow {AB} {\rm{ \;}} = (3;1;1)\) 

D. \(\overrightarrow {AB} {\rm{ \;}} = ( - 3;0;1)\)

Câu 7: Tập nghiệm của bất phương trình \({\mkern 1mu} {\log _{\dfrac{1}{2}}}{x^2} \le {\log _{\dfrac{1}{{\sqrt 2 }}}}\left( {2x - 1} \right)\) là

A. \(\left( {\dfrac{1}{2};{\mkern 1mu} {\mkern 1mu} 1} \right]\)

B. \(\left( {\dfrac{1}{4};{\mkern 1mu} {\mkern 1mu} 1} \right]\)

C. \(\left[ {\dfrac{1}{4};{\mkern 1mu} {\mkern 1mu} 1} \right]\)

D. \(\left[ {\dfrac{1}{2};{\mkern 1mu} {\mkern 1mu} 1} \right]\)

Câu 8: Đồ thị hàm số \(y = {x^4} - 3{x^2} - 4\) cắt trục hoành tại bao nhiêu điểm?

A. 3

B. 2

C. 4

D. 1

Câu 9: Số nghiệm thực của phương trình \({\log _4}{x^2} = {\log _2}\left( {{x^2} - 2} \right)\) là: 

A. 0 

B. 2  

C. 4 

D. 1 

Câu 10: Có bao nhiêu giá trị nguyên của m để đồ thị hàm số \(y = {x^3} - 12x + 1 - m\) cắt trục hoành tại 3 điểm phân biệt? 

A. 3  

B. 33  

C. 32  

D. 31 

Câu 11: Biết \({\log _2}5 = a\). Khi đó \(\log 5\) bằng:

A. \(\dfrac{1}{a}\).

B. \(a + 1\).

C. \(\dfrac{a}{{a + 1}}\).

D. \(\dfrac{{a + 1}}{a}\).

Câu 12: Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh \(a\sqrt 2 .\) Cạnh bên \(SA\) vuông góc với đáy. Góc giữa \(SC\) và mặt phẳng đáy bằng \({45^0}.\) Gọi E là trung điểm của \(BC.\) Tính khoảng cách giữa hai đường thẳng \(DE\) và \(SC.\)

A. \(\dfrac{{2a\sqrt {19} }}{{19}}\)   

B. \(\dfrac{{a\sqrt {10} }}{{19}}\)     

C. \(\dfrac{{a\sqrt {10} }}{5}\)    

D. \(\dfrac{{2a\sqrt {19} }}{5}\)

Câu 13: Có bao nhiêu giá trị nguyên dương của m không vượt quá 2021 để phương trình \({4^{x - 1}} - m{.2^{x - 2}} + 1 = 0\) có nghiệm?

A. \(2019\)  

B. \(2018\) 

C. \(2021\) 

D. 2017 

Câu 14: Tính giá trị của biểu thức \(I = \int\limits_0^{\dfrac{\pi }{3}} {\cos 4xdx} \).

A. \(\dfrac{{ - \sqrt 3 }}{8}\)

B. \(\dfrac{{ - \sqrt 3 }}{{10}}\)

C. \(\dfrac{{\sqrt 3 }}{{10}}\)

D. \(\dfrac{{\sqrt 3 }}{8}\)

Câu 15: Biết rằng \({\log _2}3 = a,{\mkern 1mu} {\mkern 1mu} {\log _2}5 = b.\) Tính \({\log _{45}}4\) theo \(a,{\mkern 1mu} {\mkern 1mu} b.\)

A. \(\dfrac{{2a + b}}{2}\)   

B. \(\dfrac{{2b + a}}{2}\)  

C. \(\dfrac{2}{{2a + b}}\)  

D. \(2ab\)

Câu 16: Có bao nhiêu số tự nhiên gồm 4 chữ số đôi một khác nhau, chia hết cho 15 và mỗi chữ số đều không vượt quá 5. 

A. 38

B. 48

C. 44   

D. 24 

Câu 17:  Một lớp học có 30 học sinh nam và 10 học sinh nữ. Giáo viên chủ nhiệm cần chọn một ban cán sự lớp gồm 3 học sinh. Tính xác suất để ban cán sự lớp có cả nam và nữ. 

A. \(\dfrac{{435}}{{988}}\)     

B. \(\dfrac{{135}}{{988}}\)     

C. \(\dfrac{{285}}{{494}}\)     

D. \(\dfrac{{5750}}{{9880}}\) 

Câu 18: Số nghiệm nguyên thuộc đoạn \(\left[ { - 99;{\mkern 1mu} {\mkern 1mu} 100} \right]\) của bất phương trình \({\left( {\sin \dfrac{\pi }{5}} \right)^x} \ge {\left( {\cos \dfrac{{3\pi }}{{10}}} \right)^{\dfrac{4}{x}}}\) là:

A. 5 

B. 101 

C. 100 

D. 4 

Câu 19: Trong không gian với hệ tọa độ \(Oxyz,\) cho đường thẳng \(\Delta :{\mkern 1mu} {\mkern 1mu} \dfrac{{x - 1}}{1} = \dfrac{{y - 2}}{2} = \dfrac{z}{{ - 2}}\) và mặt phẳng \(\left( P \right):{\mkern 1mu} {\mkern 1mu} 2x - y + 2z - 3 = 0.\) Gọi α là góc giữa đường thẳng Δ và mặt phẳng (P). Khẳng định nào sau đây là đúng? 

A. \(\cos \alpha  =  - \dfrac{4}{9}\)

B. \(\sin \alpha  = \dfrac{4}{9}\)

C. \(\cos \alpha  = \dfrac{4}{9}\)

D. \(\sin \alpha  =  - \dfrac{4}{9}\)

Câu 20: Cho cấp số cộng \(\left( {{u_n}} \right)\) thỏa mãn \({u_1} + {u_{2020}} = 2,\) \({u_{1001}} + {u_{1221}} = 1.\) Tính \({u_1} + {u_2} + .... + {u_{2021}}.\)

A. \(\dfrac{{2021}}{2}\) 

B. 2021 

C. 2020 

D. 1010 

Câu 21: Trong không gian với hệ tọa độ \(Oxyz,\) cho đường thẳng \(\Delta :{\mkern 1mu} {\mkern 1mu} \dfrac{{x - 1}}{2} = \dfrac{{y - 2}}{{ - 2}} = \dfrac{{z - 3}}{1}\) và điểm \(A\left( { - 1;{\mkern 1mu} {\mkern 1mu} 2;{\mkern 1mu} {\mkern 1mu} 0} \right).\) Khoảng cách từ điểm A đến đường thẳng Δ bằng: 

A. \(\dfrac{{\sqrt {17} }}{9}\)

B. \(\dfrac{{\sqrt {17} }}{3}\)

C. \(\dfrac{{2\sqrt {17} }}{9}\)

D. \(\dfrac{{2\sqrt {17} }}{3}\)

Câu 22: Tìm các số thực a,b thỏa mãn \(2a + (b + i)i = 1 + 2i\) với \(i\) là đơn vị ảo.

A. \(a = 0,b = 1.\)

B. \(a = 1,b = 2.\)

C. \(a = 0,b = 2.\)

D. \(a = \dfrac{1}{2},b = 1.\)

Câu 23: Trong không gian với hệ tọa độ \(Oxyz,\) cho đường thẳng \(\Delta :{\mkern 1mu} {\mkern 1mu} \dfrac{{x - 1}}{1} = \dfrac{{y + 1}}{1} = \dfrac{z}{2}\) và hai mặt phẳng \(\left( P \right):{\mkern 1mu} {\mkern 1mu} x - 2y + 3z = 0,\left( Q \right):{\mkern 1mu} {\mkern 1mu} x - 2y + 3z + 4 = 0.\) Viết phương trình mặt cầu có tâm thuộc đường thẳng \(\Delta \) và tiếp xúc với cả hai mặt phẳng \(\left( P \right)\) và \(\left( Q \right).\)

A. \({x^2} + {\left( {y - 2} \right)^2} + {\left( {z - 2} \right)^2} = \dfrac{1}{7}\)

B. \({x^2} + {\left( {y + 2} \right)^2} + {\left( {z + 2} \right)^2} = \dfrac{1}{7}\)

C. \({x^2} + {\left( {y + 2} \right)^2} + {\left( {z + 2} \right)^2} = \dfrac{2}{7}\)

D. \({x^2} + {\left( {y - 2} \right)^2} + {\left( {z - 2} \right)^2} = \dfrac{2}{7}\)

Câu 24: Tìm nguyên hàm \(\int {\left( {2x - 1} \right)\ln xdx} \). 

A. \(\left( {{x^2} - x} \right)\ln x + \dfrac{{{x^2}}}{2} - x + C\)

B. \(\left( {{x^2} - x} \right)\ln x - \dfrac{{{x^2}}}{2} + x + C\)

C. \(\left( {{x^2} - x} \right)\ln x - \dfrac{{{x^2}}}{2} - x + C\)

D. \(\left( {{x^2} - x} \right)\ln x + \dfrac{{{x^2}}}{2} + x + C\)

Câu 25: Phương trình \({\log _2}\left( {3x + 1} \right) = 2\) có nghiệm là

A. \(x = 1\)

B. \(x = 2\)

C. \(x = 3\)

D. \(x = 4\)

Câu 26: Cho hàm số \(y = m{x^3} + m{x^2} - \left( {m + 1} \right)x + 1\). Tìm tất cả các giá trị của m để hàm số nghịch biến trên R? 

A. \( - \dfrac{3}{4} < m < 0\)

B. \(m \le 0\)

C. \( - \dfrac{3}{4} \le m \le 0\)

D. \(m \le  - \dfrac{3}{4}\)

Câu 27: Có bao nhiêu giá trị nguyên dương của m để hàm số \(y = {x^2} + 8\ln 2x - mx\) đồng biến trên \(\left( {0; + \infty } \right)\)? 

A. 6  

B. 7  

C. 5  

D. 8 

Câu 28: Trong không gian với hệ tọa độ Oxyz, cho các điểm \(A\left( {1;0;2} \right)\), \(B\left( { - 1;1;3} \right)\), \(C\left( {3;2;0} \right)\) và mặt phẳng \(\left( P \right):{\mkern 1mu} {\mkern 1mu} x + 2y - 2z + 1 = 0\). Biết rằng điểm \(M\left( {a;b;c} \right)\) thuộc mặt phẳng (P) sao cho biểu thức \(M{A^2} + 2M{B^2} - M{C^2}\) đạt giá trị nhỏ nhất. Khi đó \(a + b + c\) bằng: 

A. \( - 1\)

B. 1 

C. 3 

D. 5 

Câu 29: Cho hàm số \(y = {x^3} - 3{x^2} + 2\). Có bao nhiêu tiếp tuyến với đồ thị hàm số đi qua điểm \(A\left( {1;0} \right)\)? 

A. 2

B. 0  

C. 1

D. 3 

Câu 30: Cho hàm số \(f\left( x \right)\) liên tục trên R và thỏa mãn \(xf'\left( x \right) + \left( {x + 1} \right)f\left( x \right) = {e^{ - x}}\) với mọi \(x\). Tính \(f'\left( 0 \right)\). 

A. 1  

B. \( - 1\)    

C. \(\dfrac{1}{e}\)

D. \(e\)

Câu 31: Tìm \(m\) để \(\left( {{C_m}} \right):{x^2} + {y^2} - 6mx + 4my - 24m + 4 = 0\) là phương trình đường tròn.

A. \( - 2 < m < \dfrac{2}{{13}}\).

B. \(m < {\rm{ \;}} - 2\).

C. \(m > \dfrac{2}{{13}}\).

D. \(\left[ {\begin{array}{*{20}{l}}{m < {\rm{ \;}} - 2}\\{m > \dfrac{2}{{13}}}\end{array}} \right.\).

Câu 32: Cho hàm số \(f\left( x \right)\) liên tục trên \(\left( {0; + \infty } \right)\) và thỏa mãn \(2f\left( x \right) + xf\left( {\dfrac{1}{x}} \right) = x\) với mọi \(x > 0\). Tính \(\int\limits_{\dfrac{1}{2}}^2 {f\left( x \right)dx} \). 

A. \(\dfrac{7}{{12}}\)    

B. \(\dfrac{7}{4}\)

C. \(\dfrac{9}{4}\)

D. \(\dfrac{3}{4}\)

Câu 33: Cho hình chóp \(S.ABC\) có \(AB = 3a,{\mkern 1mu} {\mkern 1mu} BC = 4a,{\mkern 1mu} {\mkern 1mu} CA = 5a\), các mặt bên tạo với đáy góc \({60^0}\), hình chiếu vuông góc của S lên mặt phẳng \(\left( {ABC} \right)\) thuộc miền trong tam giác ABC. Tính thể tích hình chóp \(S.ABC\).

A. \(2{a^3}\sqrt 3 \)      

B. \(6{a^3}\sqrt 3 \)       

C. \(12{a^3}\sqrt 3 \)     

D. \(2{a^3}\sqrt 2 \)

Câu 34: Cho khối lăng trụ tam giác đều \(ABC.A'B'C'\) có cạnh đáy là \(2a\) và khoảng cách từ điểm A đến mặt phẳng \(\left( {A'BC} \right)\) bằng a. Tính thể tích của khối lăng trụ \(ABC.A'B'C'\). 

A. \(\dfrac{{\sqrt 2 {a^3}}}{3}\)       

B. \(\dfrac{{{a^3}\sqrt 2 }}{2}\)       

C. \(2\sqrt 2 {a^3}\)       

D. \(\dfrac{{3{a^3}\sqrt 2 }}{2}\)

Câu 35: Tìm tập hợp các điểm biểu diễn số phức z thỏa mãn \(\left| {z - 1 + 3i} \right| = \left| {\bar z + 1 - i} \right|\). 

A. \(x - 2y - 2 = 0\)

B. \(x + y - 2 = 0\)

C. \(x - y + 2 = 0\)

D. \(x - y - 2 = 0\)

Câu 36: Cho hàm số \(y = f\left( x \right)\) có đạo hàm liên tục trên \(\left[ {1;2} \right]\), thỏa mãn \(f\left( x \right) = x.f'\left( x \right) - {x^2}\). Biết \(f\left( 1 \right) = 3\), tính \(f\left( 2 \right)\).

Đáp án:

Câu 37: Cho một hình trụ thay đổi nội tiếp trong một hình nón cố định cho trước (tham khảo hình vẽ bên). Gọi thể tích các khối nón và khối trụ tương ứng là V và V’. Biết rằng V’ là giá trị lớn nhất đạt được, khi đó tỉ số \(\dfrac{{V'}}{V}\) bằng bao nhiêu?

Đáp án:

Câu 38: Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC có \(A\left( {1;1} \right),\) \(B\left( {0;3} \right)\) và \(C\left( {4;0} \right)\). Chiều cao của tam giác kẻ từ đỉnh A bằng:

Đáp án:

Câu 39: Cho phương trình \({\log _{\dfrac{1}{2}}}\left( {2x - m} \right) + {\log _2}\left( {3 - x} \right) = 0\), m là tham số. Hỏi có bao nhiêu giá trị nguyên dương của m để phương trình có nghiệm?

Đáp án:

Câu 40: Trong không gian tọa độ \(Oxyz\), cho điểm \(M(1;2; - 3)\). Hình chiếu của M tương ứng lên \(Ox,Oy,Oz,(Oyz),(Ozx),(Oxy)\) là \(A,B,C,D,E,F\). Gọi P và Q tương ứng là giao điểm của đường thẳng OM với các mặt phẳng \((ABC)\) và \((DEF)\). Độ dài \(PQ = \dfrac{{\sqrt a }}{b}\). Tính \(a + b\).

Đáp án:

Câu 41: Giả sử \({\left( {1 + x + {x^2} + {x^3}} \right)^4} = {a_0} + {a_1}x + {a_2}{x^2} + ... + {a_{12}}{x^{12}}{\mkern 1mu} {\mkern 1mu} \left( {{a_i} \in \mathbb{R}} \right)\)(ai∈R). Giá trị của tổng \(S = C_4^0{a_4} - C_4^1{a_3} + C_4^2{a_2} - C_4^3{a_1} + C_4^4{a_0}\) bằng

Đáp án: 

Câu 42: Tìm số nghiệm của phương trình \(\sin \left( {\cos x} \right) = 0\) trên đoạn \(\left[ {1;2021} \right]\).

Đáp án:

Câu 43: Cho hàm số \(f\left( x \right)\) xác định trên R, thỏa mãn \(f'\left( x \right) = 2x - 1\) và \(f\left( 3 \right) = 5\). Giả sử phương trình \(f\left( x \right) = 999\) có hai nghiệm \({x_1}\) và \({x_2}\). Tính tổng \(S = \log \left| {{x_1}} \right| + \log \left| {{x_2}} \right|\).

Đáp án:

Câu 44: Trong không gian \(Oxyz\), cho hai điểm \(M(1;5; - 2)\) và \(.\left\{ {\begin{array}{*{20}{l}}{x = 1 + 3t}\\{y = 5 - 6t}\\{z =  - 2 + t}\end{array}} \right.\) Xét hai điểm \(M( - 4;3)\) và \(N\) thay đổi thuộc mặt phẳng \((Oxy)\) sao cho \(MN = 3\). Giá trị lớn nhất của \(|AM - BN|\) =x, Tính giá trị của \({x^2}\)

Đáp án:

Câu 45: Cho hình lăng trụ đều ABC.A’B’C’, tất cả các cạnh có độ dài bằng a. Gọi M là trung điểm của cạnh BC. Biết khoảng cách giữa hai đường thẳng AM và BC’ là d

Tìm \({\left( {\dfrac{d}{a}} \right)^2}\).\(\)

Đáp án:

XEM TOÀN BỘ ĐỀ