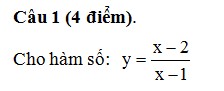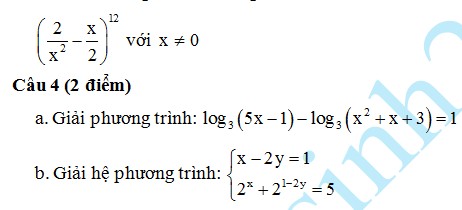Đề thi thử THPT Quốc gia môn Toán 2015 THPT chuyên Thăng Long
11/03/2015 09:48 am
Đề thi thử THPT Quốc gia năm 2015 môn Toán của trường THPT chuyên Thăng Long, Hà Nội có đáp án chi tiết.
Đề thi thử THPT Quốc gia môn Toán trường THPT chuyên Thăng Long năm 2015
a. Khảo sát sự biến thiên và vẽ đồ thị của hàm số b. Tìm các giá trị của m để đường thẳng d: y = m + 1 -x cắt đồ thị hàm số tại 2 điểm A, B sao cho độ dài đoạn thẳng AB = 2√2 Câu 2 (2 điểm). Giải phương trình: sin2x + √3 cos2x = 2 cosx - √3 Câu 3 (2 điểm) a. Hộp thứ nhất chứa 10 viên bi kích thước khác nhau, trong đó có 4 viên bi màu đỏ và 6 viên bi màu xanh. Hộp thứ hai chứa 12 viên bi kích thước khác nhau, trong đó có 7 viên bi màu dỏ và 5 viên bi màu xanh. Lấy ngẫu nhiên ở mỗi hộp 3 viên bi. Tính sác xuất để lấy được 6 viên bi cùng một màu. b. Tìm số hạng chứa x6 trong khai triển nhị thức Niu - ton của
Câu 5 (4 điểm) Cho hình chóp S. ABCD có đáy ABCD là hình chữ nhật với AB = a; AD = 2a và SA ⊥ (ABCD) ; góc giữa đường thẳng SB và mặt phẳng (ABCD) bằng 450. Gọi M là trung điểm BC và N là trung điểm của SC a. Tính thể tích khối chóp S.ABCD, tính thể tích khối tứ diện NMCD b. Tính khoảng cách giữa hai đường thẳng BD và SC. Tính cosin góc giữa hai mặt phẳng (SBC) và (SDC) Câu 6 (2,0 điểm). Trong mặt phẳng với hệ tọa độ Oxy, cho hình vuông ABCD. Trên các cạch BC, CD và DA lần lượt lấy các điểm M, N và E sao cho CM = DN = DE = 1/3 BC . Gọi H là giao điểm của AN và DM, biết H (9/10; 13/10) và E(0;2). Viết phương trình đường thẳng BH và tìm tọa độ điểm B
Đáp án đề thi thử THPT Quốc gia môn Toán trường THPT chuyên Thăng Long năm 2015
Xem đáp án đầy đủ trường chuyên Thăng Long - Hà Nội tại đây: http://tuyensinh247.com/de-thi-thu-thpt-quoc-gia-mon-toan-truong-thpt-chuyen-thang-long-ha-noi-nam-2015-t2-ic1162.html?course_id=55 Tuyensinh247 tổng hợp 🔥 2K9 CHÚ Ý! LUYỆN THI TN THPT - ĐÁNH GIÁ NĂNG LỰC - ĐÁNH GIÁ TƯ DUY!
️🎯 LỘ TRÌNH SUN 2027 - LUYỆN THI TN THPT - ĐGNL - ĐGTD (3IN1)
|
>> Đề thi THPT Quốc gia môn Toán THPT Đa Phúc năm 2015
Viết bình luận: Đề thi thử THPT Quốc gia môn Toán 2015 THPT chuyên Thăng Long
- Hướng dẫn giải môn Tin đề thi khảo sát lớp 12 - Hà Nội 2026 (13/03/2026)
- Hướng dẫn giải Đề thi khảo sát lớp 12 môn Địa 2026 - Sở GD Hà Nội (13/03/2026)
- Hướng dẫn giải Đề thi khảo sát lớp 12 môn Sinh 2026 - Sở GD Hà Nội (13/03/2026)
- Hướng dẫn giải môn Anh Đề thi khảo sát lớp 12 - Hà Nội 2026 (13/03/2026)
Tin tức mới nhất
- Học sinh chưa có hộ khẩu tại Hà Nội vẫn được thi lớp 10 công lập 2026
- Đại học Cần Thơ tăng chỉ tiêu tuyển sinh 2026
- Hướng dẫn giải môn Tin đề thi khảo sát lớp 12 - Hà Nội 2026
- Hướng dẫn giải Đề thi khảo sát lớp 12 môn Địa 2026 - Sở GD Hà Nội
- Hướng dẫn giải Đề thi khảo sát lớp 12 môn Sinh 2026 - Sở GD Hà Nội
- Hướng dẫn giải môn Anh Đề thi khảo sát lớp 12 - Hà Nội 2026