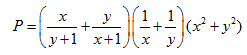Đề thi thử THPTQG môn Toán - THPT Phan Đăng Lưu năm 2015
05/04/2015 16:54 pm
Đề thi thử THPTQG môn Toán - THPT Phan Đăng Lưu năm 2015, các em tham khảo dưới đây:
Câu1 (2,0 điểm). Cho hàm số a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số (1). b) Viết phương trình tiếp tuyến của (C), biết tiếp tuyến vuông góc với đường thẳng Câu 2 (1,0 điểm). a) Giải phương trình b) Giải bất phương trình Câu 3 (1,0 điểm). Tính tích phân
Câu 4 (1,0 điểm). a) Cho số phức z thỏa mãn b) Tìm hệ số của trong khai triển nhị thứcNewtoncủa Câu 5 (1,0 điểm). Trong không gian với hệ tọa độ Oxyz, cho hai mặt phẳng (P), (Q) lần lượt có phương trình: x + 2y + 2z – 1 = 0, x + 2y – z – 3 = 0 Mặt cầu (S) có phương trình:
Viết phương trình mặt phẳng () vuông góc với (P) và (Q) đồng thời tiếp xúc với mặt cầu (S). Câu 6 (1,0 điểm). Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, AB = a, AC = 2a. Mặt bên (SBC) là tam giác cân tại S và nằm trong mặt phẳng vuông góc với đáy. Biết góc giữa mặt phẳng (SAB) và mặt phẳng (ABC) bằng 300. Tính thể tích khối chóp S.ABC và khoảng cách giữa hai đường thẳng AB và SC theo a. Câu 7 (1,0 điểm). Trong mặt phẳng với hệ tọa độ Oxy, cho hình vuông ABCD có đỉnh A(- 3; 5) và có diện tích bằng 25. Tìm tọa độ các đỉnh B, C, D của hình vuông biết tâm I của hình vuông nằm trên đường thẳng d: x + y – 5 = 0 và có hoành độ dương. Câu 8 (1,0 điểm). Giải phương trình sau trên tập hợp số thực
Câu 9 (1,0 điểm). Cho ,là hai số thực dương thỏa mãn
Tìm giá trị nhỏ nhất của biểu thức :
Đáp án sẽ được Tuyensinh247 cập nhật sau, các em chú ý theo dõi. Nguồn: THPT Phan Đăng Lưu
🔥 2K8 CHÚ Ý! LUYỆN THI TN THPT - ĐÁNH GIÁ NĂNG LỰC - ĐÁNH GIÁ TƯ DUY!
LỘ TRÌNH SUN 2026 - LUYỆN THI TN THPT - ĐGNL - ĐGTD (3IN1)
|
||
>> Đề thi thử THPT Quốc gia môn Toán chuyên Hưng Yên năm 2015
>> Đề thi thpt quốc gia 2015 Môn toán - Bộ giáo dục - Đề mẫu
1 bình luận: Đề thi thử THPTQG môn Toán - THPT Phan Đăng Lưu năm 2015
- Đề thi thử TN THPT 2026 môn Toán lần 2 - THPT Trần Phú Hoàn Kiếm (02/03/2026)
- Đề thi thử tốt nghiệp THPT môn Lý 2026 - Liên trường THPT Hà Nội (lần 1) (02/03/2026)
- Đề thi thử tốt nghiệp THPT 2026 môn Toán lần 1 - Liên trường THPT Hà Nội (02/03/2026)
- Đề thi thử tốt nghiệp THPT môn Địa 2026 - THPT Nguyễn Trãi lần 1 (02/03/2026)
Tin tức mới nhất
- Phó chủ tịch Quốc hội: Siết dạy thêm khiến phụ huynh tốn kém hơn
- Đề thi thử TN THPT 2026 môn Toán lần 2 - THPT Trần Phú Hoàn Kiếm
- Đề thi thử tốt nghiệp THPT môn Lý 2026 - Liên trường THPT Hà Nội (lần 1)
- Đề thi thử tốt nghiệp THPT 2026 môn Toán lần 1 - Liên trường THPT Hà Nội
- Đề thi thử tốt nghiệp THPT môn Địa 2026 - THPT Nguyễn Trãi lần 1
- Đề thi thử vào lớp 10 môn Toán 2026 - THCS Quang Trung
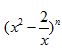 , biết rằng n là số nguyên dương thỏa mãn
, biết rằng n là số nguyên dương thỏa mãn