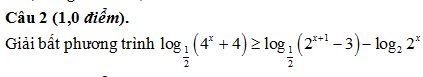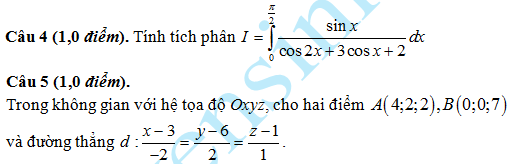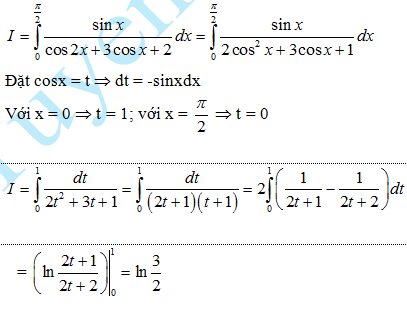Đề thi thử THPT Quốc gia môn Toán chuyên Hưng Yên năm 2015
26/03/2015 15:41 pm
Đáp án đề thi thử THPT Quốc gia môn Toán trường THPT chuyên Hưng Yên năm 2015, được Tuyensinh247 cập nhật thứ năm, ngày 26/3/2015.
|
Đề thi thử THPT Quốc gia môn Toán THPT chuyên Hưng Yên năm 2015 Câu 1 (2,0 điểm). Cho hàm số y = x3 + 3mx2 + 2 (1), với m là tham số thực. a) Khảo sát sự biến thiên và vẽ đồ thị hàm số (1) khi m = 1. b) Tìm m để đồ thị hàm số (1) có hai điểm cực trị A, B sao cho diện tích tam giác OAB bằng 2 (O là gốc tọa độ).
Câu 3 (1,0 điểm). a) Gọi A, B là hai điểm biểu diễn cho các số phức là nghiệm của phương trình z2 + 2z + 3 = 0. Tính độ dài đoạn thẳng AB. b) Trong kì thi THPT Quốc gia năm 2015, mỗi thí sinh có thể dự thi tối đa 8 môn: Toán, Lý, Hóa, Sinh, Văn, Sử, Địa và Tiếng anh. Một trường Đại học dự kiến tuyển sinh dựa vào tổng điểm của 3 môn trong kì thi chung và có ít nhất 1 trong hai môn là Toán hoặc Văn. Hỏi trường Đại học đó có bao nhiêu phương án tuyển sinh?
Chứng minh rằng hai đường thẳng d và AB cùng thuộc một mặt phẳng. Tìm điểm C thuộc đường thẳng d sao cho tam giác ABC cân đỉnh A. Câu 6 (1,0 điểm). Cho lăng trụ đứng ABC.A’B’C’có đáy là tam giác cân, AB = AC = a, góc BAC = 1200. Mặt phẳng (AB’C’) tạo với mặt đáy góc 600. Tính thể tích lăng trụ ABC.A'B'C' và khoảng cách từ đường thẳng đến mặt phẳng (AB’C’) theo . Câu 7 (1,0 điểm). Trong mặt phẳng với hệ tọa độ Oxy, cho hình vuông ABCD có A (-1;2). Gọi M, N lần lượt là trung điểm của cạnh AD và DC; K là giao điểm của BN với CM. Viết phương trình đường tròn ngoại tiếp tam giác BMK, biết BN có phương trình 2x + y – 8 = 0 và điểm B có hoành độ lớn hơn 2.
Đáp án đề thi thử THPT Quốc gia môn Toán THPT chuyên Hưng Yên năm 2015 Câu 3:
Câu 4:
Xem đáp án đầy đủ tại đây: http://tuyensinh247.com/de-thi-thu-thpt-quoc-gia-mon-toan-truong-thpt-chuyen-hung-yen-nam-hoc-2015-t2-ic1206.html?course_id=55 Tuyensinh247 tổng hợp 🔥 2K8 CHÚ Ý! LUYỆN THI TN THPT - ĐÁNH GIÁ NĂNG LỰC - ĐÁNH GIÁ TƯ DUY!
LỘ TRÌNH SUN 2026 - LUYỆN THI TN THPT - ĐGNL - ĐGTD (3IN1)
|
4 bình luận: Đề thi thử THPT Quốc gia môn Toán chuyên Hưng Yên năm 2015
- Đề thi thử TN THPT 2026 môn Toán lần 2 - THPT Trần Phú Hoàn Kiếm (02/03/2026)
- Đề thi thử tốt nghiệp THPT môn Lý 2026 - Liên trường THPT Hà Nội (lần 1) (02/03/2026)
- Đề thi thử tốt nghiệp THPT 2026 môn Toán lần 1 - Liên trường THPT Hà Nội (02/03/2026)
- Đề thi thử tốt nghiệp THPT môn Địa 2026 - THPT Nguyễn Trãi lần 1 (02/03/2026)
Tin tức mới nhất
- Phó chủ tịch Quốc hội: Siết dạy thêm khiến phụ huynh tốn kém hơn
- Đề thi thử TN THPT 2026 môn Toán lần 2 - THPT Trần Phú Hoàn Kiếm
- Đề thi thử tốt nghiệp THPT môn Lý 2026 - Liên trường THPT Hà Nội (lần 1)
- Đề thi thử tốt nghiệp THPT 2026 môn Toán lần 1 - Liên trường THPT Hà Nội
- Đề thi thử tốt nghiệp THPT môn Địa 2026 - THPT Nguyễn Trãi lần 1
- Đề thi thử vào lớp 10 môn Toán 2026 - THCS Quang Trung