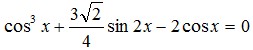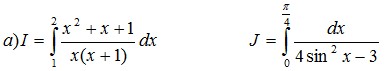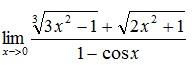Đề thi thử đại học môn Toán khối D năm 2014

ĐỀ THI THỬ ĐẠI HỌC MÔN TOÁN KHỐI D NĂM 2014

I.PHẦN CHUNG CHO TÁT CẢ THÍ SINH: (7đ)

Câu 1:

Cho hàm số: y = -x⁴/4+ 2x² + 1 (C) 

1.Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số.

2) Định m để phương trình x⁴ – 8x²+ 4m – 4 = 0 có 4 nghiệm theo thứ tự lập thnahf cấp số cộng.

Câu 2:

1)Giải phương trình: 

2) Cho phương trình (m-3)9^x +2(m+1)3^x-(m+1) = 0. Định m để phương trình có đúng 2 nghiệm

Câu 3: Tính các tích phân

Câu 4:Cho khối chóp tam giác đều có chiều cao h ; góc đáy của mặt bên là a . Tính theo h và a thể tích của khối chop trên.

Câu 5:Cho x,yl à các số thực . Tìm GTNN của biểu thức

II.PHẦN TỰ CHỌN:

A-THEO CHƯƠNG TRÌNH CHUẨN:

Câu 6A:Trong hệ tọa độ cho hình thoi cạnh có phương trình là: hai đỉnh lần lượt thuộc các đường thẳng d₁: x + y – 8 = 0 ; d₂ : x – 2y + 3 = 0. Tìm tọa độ các đỉnh của hình thoi biết rằng diện tích hình thoi bằng 75 và đỉnh A có hoành độ âm.

Câu 7A:Trong không gian Oxyz cho 3 điểm A(0 1 ; 3 ; 4)  B(-2 ; 3 ; 3)   C(-1 ; 2;3) . Viết phương trình mặt câu (S) có tâm thuộc mp P: 4x + y +2z = 9 = 0

Câu 8A:.Không dùng máy tính cầm tay ,tính giá trị của biểu thức A= 1.1!+2.2!+3.3!+….+n.n!  (n; là số nguyên dương)

B-THEO CHƯƠNG TRÌNH NÂNG CAO:

Câu 6B: Trong hệ tọa độ  cho hai đường thẳng d₁: x - y - 2 = 0 và d₂: x + 2y - 2 = 0 . Giả sử  cắt  tại  Viết phương trình đường thẳng ∆ đi qua M ( -1; 1) cắt  d₁ , d₂  và tương ứng tại A,B sao cho AB = 3IA.

Câu 7B: Trong không gian Oxyz cho 2 đường thẳng

 và  

 và điểm I (0 ; 4 ; 3/2) ,Chứng tỏ (d₁) và (d₂) chéo nhau. Viết phương trình của đường thẳng (∆) cắt (d₁) và (d₂) tại A và B sao cho I là  trung điểm của AB

Câu 8B:.Tìm

- HẾT -

ĐÁP ÁN ĐỀ THI THỬ ĐẠI HỌC MÔN TOÁN KHỐI D NĂM 2014

Các em chú ý theo dõi các đề thi thử đại học tiếp theo trên Tuyensinh247 nhé!

Tuyensinh247 tổng hợp