Đề thi vào lớp 10 môn Toán Thanh Hóa năm 2014
30/06/2014 10:56 am
Đề thi tuyển sinh vào lớp 10 tỉnh Thanh Hóa môn Toán năm 2014 có đáp án được cập nhật thứ hai ngày 30/6/2014, các em tham khảo dưới đây.
Đề thi tuyển sinh 10 môn Toán tỉnh Thanh Hóa năm 2014 - Đề ASỞ GIÁO DỤC VÀ ĐÀO TẠO KỲ THI TUYỂN SINH VÀO LỚP 10 THPT TỈNH THANH HÓA Năm học 2014 – 2015 ĐỀ CHÍNH THỨC MÔN THI: Toán Đề A Ngày thi: 30 tháng 6 năm 2014 Câu 1: (2,0 điểm)
a. x – 2 = 0 b. x2 – 6x + 5 = 0
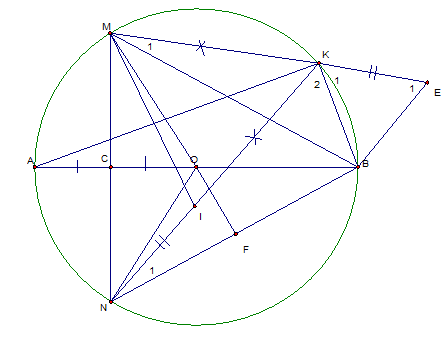
1. Rút gọn A. 2. Tính giá trị của biểu thức A khi x = 4 + 2√3 Câu 3: (2,0 điểm) Trong mặt phẳng tọa độ Oxy cho đường thẳng (d): tham số m và Parabol (P): y = x2. 1. Tìm m để đường thẳng (d) đi qua điểm A(1; 0). 2. Tìm m để đường thẳng (d) cắt Parabol (P) tại hai điểm phân biệt có hoàng độ lần lượt là x1, x2 thỏa mãn |x1 = x2| = 2 Câu 4: (3,0 điểm) Cho đường tròn tâm O đường kính AB = 2R. Gọi C là trung điểm của OA; qua C kẻ đường thẳng vuông góc với OA cắt đường tròn đó tại hai điểm phân biệt M và N. Trên cung nhỏ BM lấy điểm K ( K khác B và M), trên tia KN lấy điểm I sao cho KI = KM. Gọi H là giao điểm của AK và MN. Chứng minh rằng: 1. Tứ giác BCHK là tứ giác nội tiếp. 2. AK.AH = R2 3. NI = BK Câu 5: (1,0 điểm) Cho các số thực dương x, y, z thỏa mãn xyz = 1. Tìm giá trị lớn nhất của biểu thức Đáp án đề thi tuyển sinh 10 môn Toán tỉnh Thanh Hóa năm 2014 - Đề ANguồn đáp án GV Nguyễn Xuân Chiến |
16 bình luận: Đề thi vào lớp 10 môn Toán Thanh Hóa năm 2014
- Đáp án đề thi vào lớp 10 môn Toán - Kiên Giang 2025 (15/06/2025)
- Đáp án đề thi vào lớp 10 Kiên Giang 2025 môn Văn (14/06/2025)
- Đáp án đề thi vào lớp 10 Hà Nội năm 2025 - Chính thức (11/06/2025)
- Sở GD TPHCM công bố đáp án đề thi vào lớp 10 năm 2025 (11/06/2025)
Tin tức mới nhất
- Danh sách trường công bố đề án tuyển sinh 2026 - Mới nhất
- Thông tin tuyển sinh Đại học Mỏ địa chất 2026
- Thông tin tuyển sinh trường Đại học Sư phạm nghệ thuật Trung Ương 2026
- Thông tin tuyển sinh Đại học Lâm nghiệp 2026
- Thông tin tuyển sinh Học viện Kỹ thuật và Công nghệ an ninh 2026
- Thông tin tuyển sinh Đại học Phòng cháy chữa cháy 2026
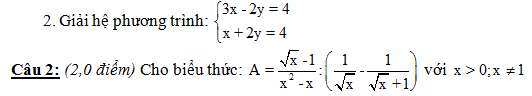

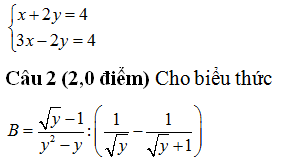
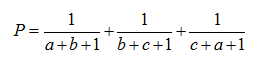 Tìm giá trị lớn nhất của biểu thức
Tìm giá trị lớn nhất của biểu thức